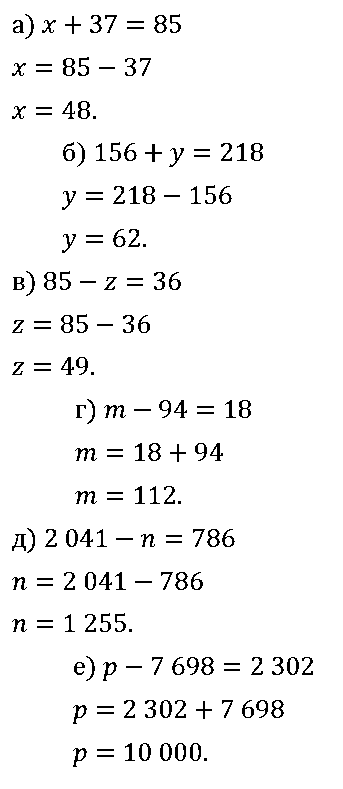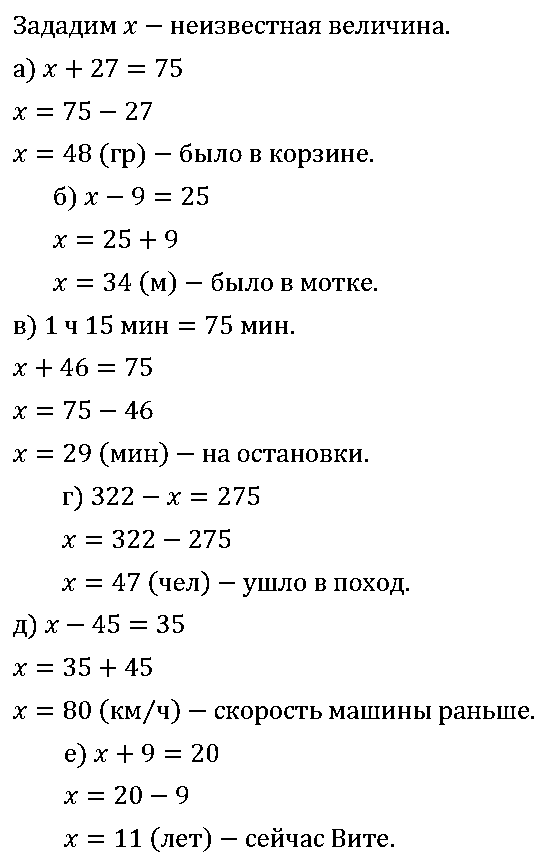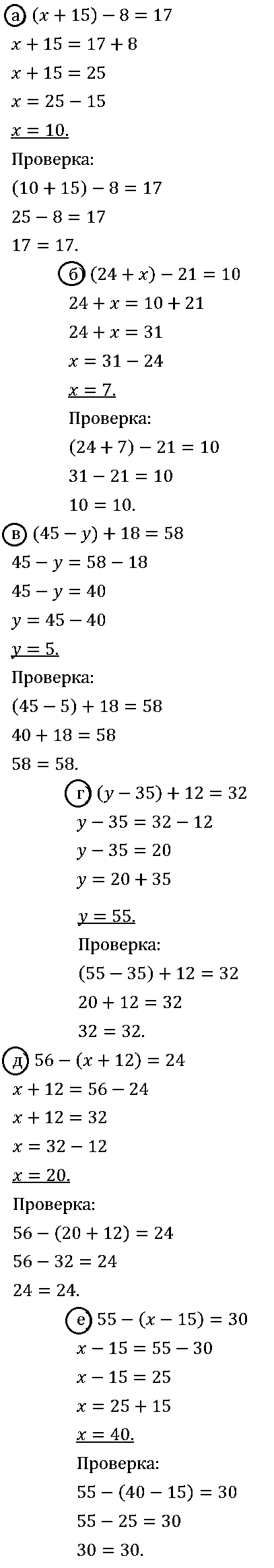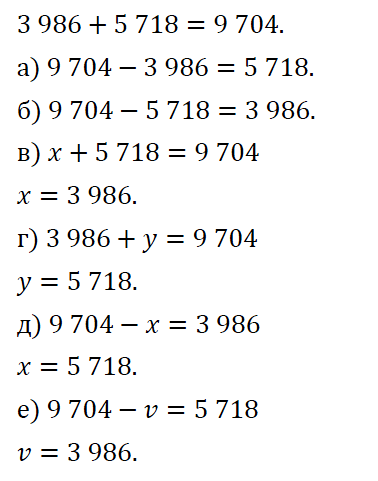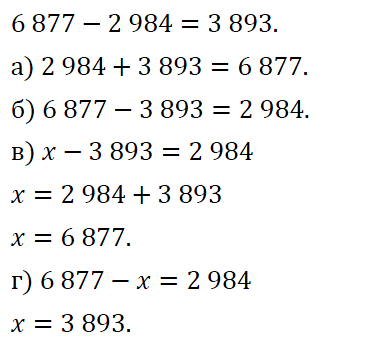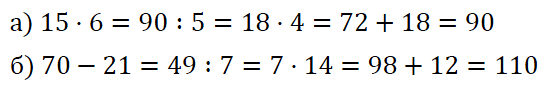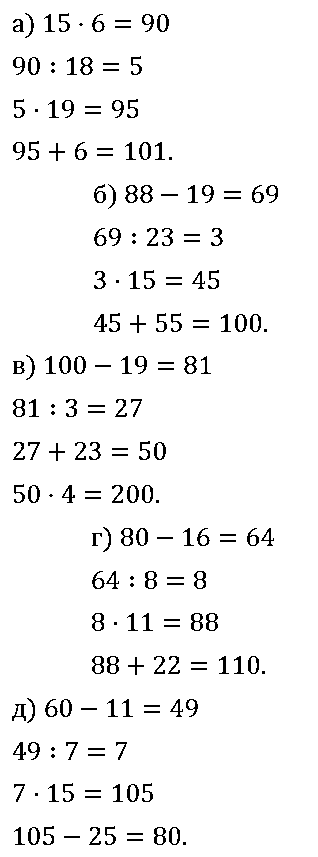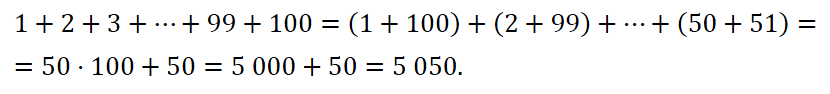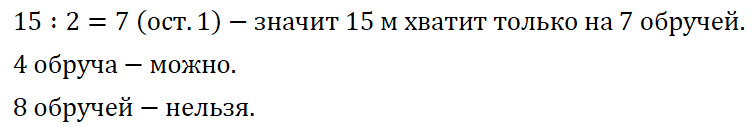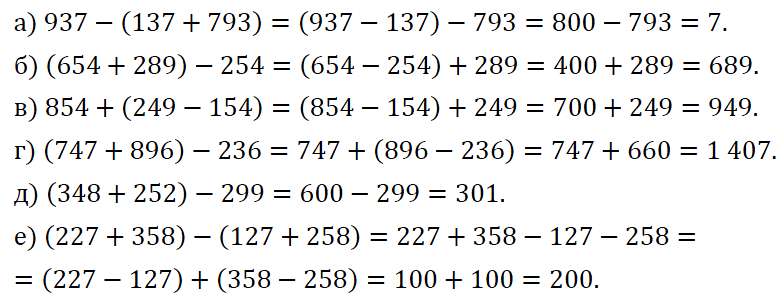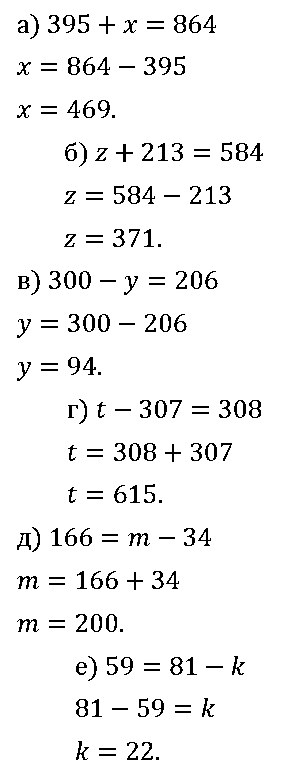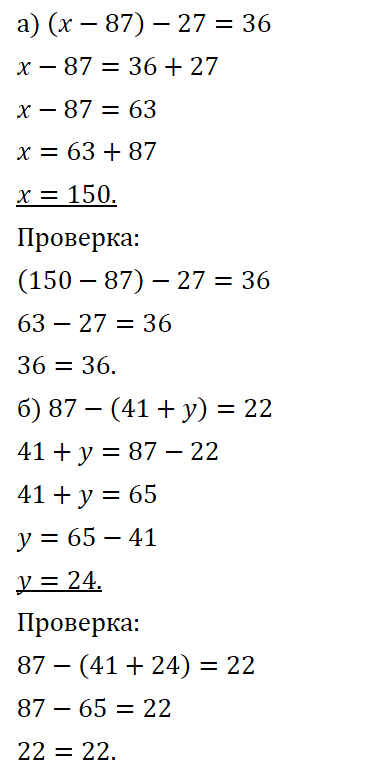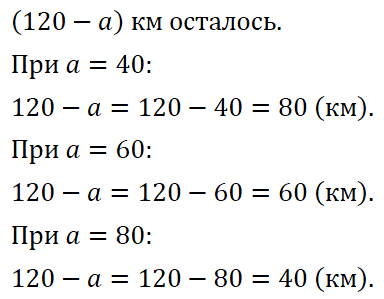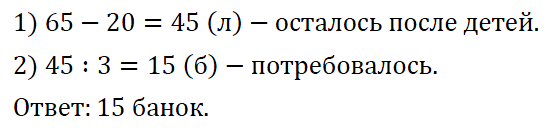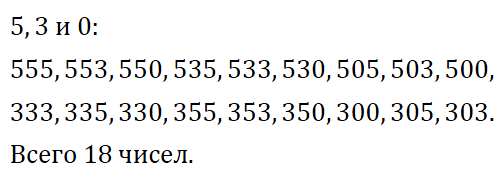Математика 5 Виленкин Упражнения 372-403 к учебнику математики с ответами. Решения задач №№ 372 — 403 из учебника УМК Виленкин и др. по теме «10. Уравнение».
Математика 5 класс. УМК Виленкин и др. Учебник
.
(упражнения №№ 372 — 403)
Вначале необходимо прочитать тему учебника «10. Уравнение«.
№ 372. Решите уравнение: а) х + 37 = 85; б) 156 + у = 218; в) 85 – z = 36; г) m – 94 = 18; д) 2041 – n = 786; е) р – 7698 = 2302.
№ 373. Решите с помощью уравнения задачу:
1) В корзине было несколько грибов. После того как в неё положили ещё 27 грибов, их стало 75. Сколько грибов было в корзине?
2) В мотке было несколько метров проволоки. После того как отрезали 9 м, осталось 25 м. Сколько метров проволоки было в мотке?
3) Электропоезд был в пути 1 ч 15 мин. Некоторое время он затратил на остановки, а двигался 46 мин. Сколько времени затрачено на остановки?
4) В спортивном лагере 322 человека. Когда несколько человек ушли в поход, в лагере осталось 275 человек. Сколько человек ушли в поход?
5) Скорость автомашины уменьшили на 45 км/ч, и она стала равной 35 км/ч. Какова была скорость машины раньше?
6) Через 9 лет Вите исполнится 20 лет. Сколько лет ему сейчас?
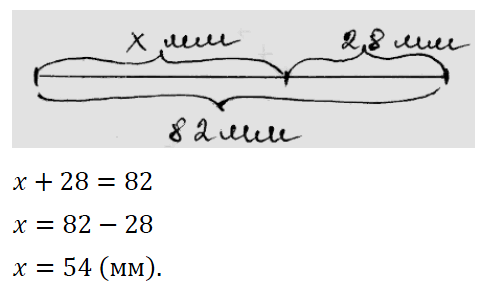
№ 374. Составьте уравнение по рисунку 45 и решите его.

№ 375. Решить уравнение (у + 64) – 38 = 48 можно двумя способами:
1) сначала найти неизвестное уменьшаемое у + 64:
у + 64 = 48 + 38, у + 64 = 86,
а потом найти неизвестное слагаемое у:
у = 86 – 64, у – 22
или
2) сначала упростить выражение, стоящее в левой части уравнения, использовав свойства вычитания:
у + 64 – 38 = 48, у + 26 = 48,
а затем найти неизвестное слагаемое у:
у = 48 – 26, у – 22.
Подобным образом решите двумя способами уравнение: а) (х + 98) + 14 = 169; б) (35 +у) – 15 = 31.

№ 376. Решите уравнение и выполните проверку:
а) (х + 15) – 8 = 17; б) (24 + х) – 21 = 10; в) (45 – у)+ 18 = 58; г) (у – 35) + 12 = 32; д) 56 – (х + 12) = 24; е) 55 – (х – 15) = 30.
№ 377. Решите с помощью уравнения задачу:
1) Витя задумал число. Если к этому числу прибавить 23 и к полученной сумме прибавить 18, то будет 52. Какое число задумал Витя?
2) Маша задумала число. Если к этому числу прибавить 14 и от полученной суммы отнять 12, то будет 75. Какое число задумала Маша?
3) В бензобак, где был бензин, перед поездкой долили ещё 39 л. Во время поездки израсходовали 43 л бензина, после чего в бензобаке осталось 27 л. Сколько литров бензина было в бензобаке первоначально?
4) В ателье было 60 м ткани. Из неё сшили платья, ещё 16 м израсходовали на детские костюмы, после чего осталось 20 м этой ткани. Сколько метров ткани пошло на платья?
№ 378. Запишите в виде равенства:
а) У Вани было х яблок, у Пети – на 8 яблок больше, а у Нины – на 3 яблока меньше, чем у Вани. Вместе у них было 41 яблоко.
б) Один токарь выточил у деталей, другой – на 7 деталей больше, чем первый, а третий – на 8 деталей меньше, чем второй. Вместе они сделали 81 деталь.
в) У Кости n открыток, у Игоря – на 8 открыток меньше, чем у Кости, а у Наташи – на 15 открыток больше, чем у Кости. У Наташи столько же открыток, сколько у Кости и Игоря вместе.
г) В первый сосуд налили т л жидкости, во второй – на 7 л меньше, чем в первый, а в третий сосуд – на 10 л больше, чем во второй. В третьем сосуде оказалось столько жидкости, сколько в первом и втором сосудах вместе.
№ 379. Сумма (3986 + 5718) равна 9704 . Пользуясь этим, найдите без вычислений значение выражения или корень уравнения:
а) 9704 – 3986; б) 9704 – 5718; в) х + 5718 = 9704; г) 3986 + у = 9704; д) 9704 –х = 3986; е) 9704 – о = 5718.
№ 380. Разность (6877 – 2984) равна 3893 . Пользуясь этим, найдите без вычислений значение выражения или решите уравнение:
а) 2984 + 3893; б) 6877 – 3893; в) х – 3893 = 2984; г) 6877 – л: = 2984.
№ 381. Вместо звёздочек в записи вычислений цепочкой поставьте необходимые числа.
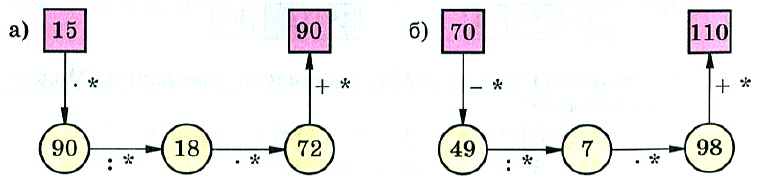
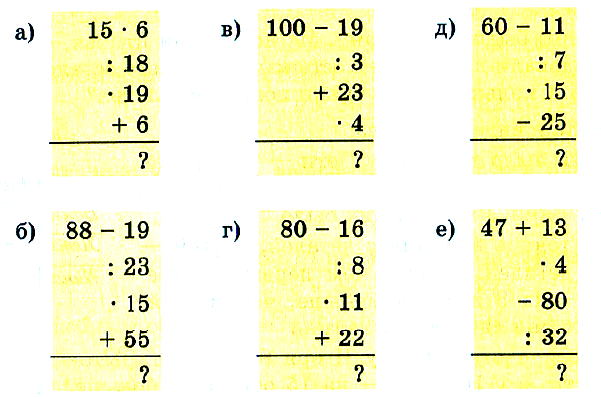
№ 382. Вычислите устно:
№ 383. На координатном луче даны точки А(18), В(7), С(31), D(27), Е{23), О(0). Какие из этих точек:
а) левее точки £ и на сколько единичных отрезков;
б) правее точки А и на сколько единичных отрезков;
в) расположены между точками В и О?
№ 384. Что больше и во сколько раз:
а) два часа или сорок минут;
б) десять центнеров или две тонны;
в) шесть сантиметров или двадцать миллиметров?
№ 385. В бидоне 24 л молока. Для приготовления завтраков израсходовали четвёртую часть молока, а для приготовления обедов – половину оставшегося молока. Сколько литров молока осталось в бидоне?
ОТВЕТ: 9 литров.
№ 386. Найдите пропущенное число:
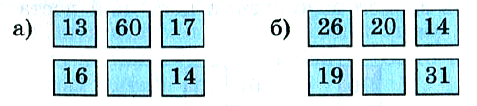
№ 387. Вместо некоторых цифр поставлены звёздочки. Можно ли сравнить числа: а) 32** и 31**; б) *1** и 8**; в) **** и ***; г) *5* и 1**?
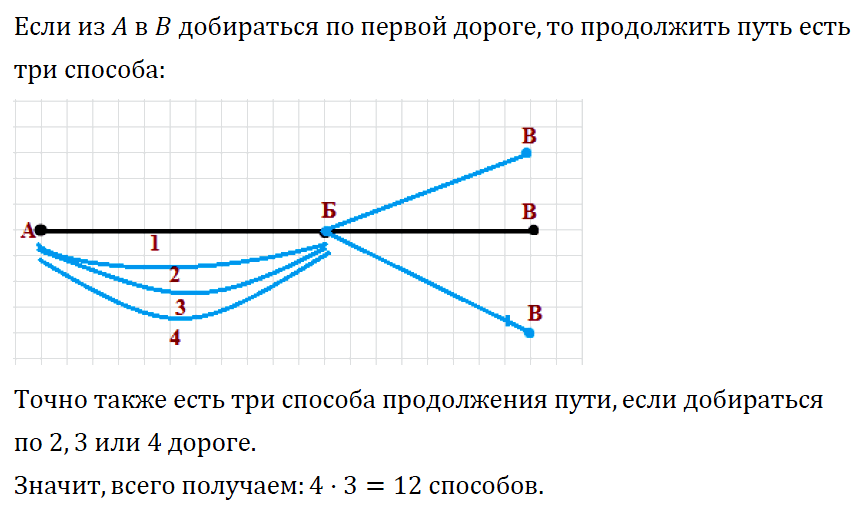
№ 388. Из села Аникеево в село Большово ведут четыре дороги, а из села Болыиово в село Виноградово – три дороги. Сколькими способами можно добраться из Аникеева в Виноградово через село Большово?
Решение. Если из А в Б добираться по 1–й дороге, то продолжить путь есть три способа:
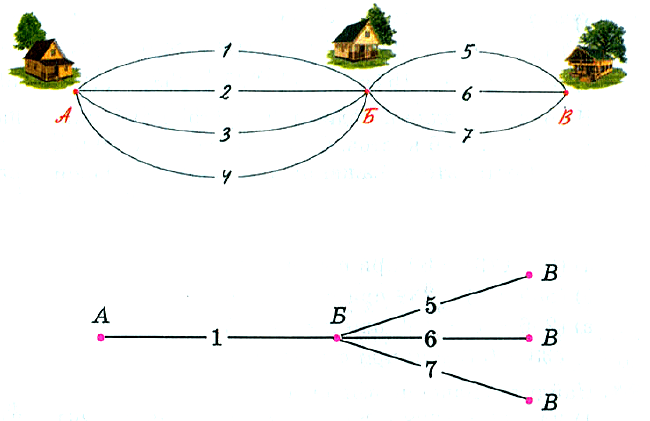
Точно так же рассуждая, получаем по три способа продолжить путь, начав добираться и по 2–й, и по 3–й, и по 4–й дороге. Значит, всего получается 4 • 3 = 12 способов добраться из Аникеева в Виноградово.
№ 389. Подумайте, как Карл Гаусс складывал числа от 1 до 100.

№ 390. Из проволоки длиной 15 м делают обручи длиной 2 м. На сколько обручей хватит проволоки? Можно ли изготовить 4 обруча? 8 обручей?
№ 391. Вычислите, выбирая удобный порядок выполнения действий:
а) 937 – (137 + 793); б) (654 + 289) – 254; в) 854 + (249 – 154); г) (747 + 896) – 236; д) (348 + 252) – 299; е) (227 + 358) – (127 + 258).
№ 392. На одной грядке посадили 30 кустов клубники, а на другой к кустов. Погибло 6 кустов. Сколько кустов клубники осталось на грядках? Составьте выражение для решения задачи и найдите его значение при k = 26; 35.
№ 393. Найдите значение выражения, предварительно упростив его:
а) (b + 179) – 89 при b = 56; 75;
б) (839 + с) – 239 при с = 37; 98;
в) (256 – х) – 156 при х = 44; 87;
г) 238 – (38 + а) при а = 78; 0.
№ 394. Найдите значение выражения:
1) 34 • 27 + 1638 : 39; 2) 32 • 37 – 3293 : 37; 3) (321 – 267) • (361 – 215) : 219; 4) (123 + 375) • 24 : (212 – 129).
№ 395. Решите уравнение:
а) 395 + х = 864; б) z + 213 = 584; в) 300 – у = 206; г) t – 307 = 308; д) 166 = m – 34; е) 59 = 81 – k.
№ 396. Решите уравнение и выполните проверку: а) (х – 87) – 27 = 36; б) 87 – (41 + у) = 22.
№ 397. Решите с помощью уравнения задачу:
1) Продолжительность дня с 7 октября до 19 ноября уменьшилась на 3 ч и стала равной 8 ч. Какой была продолжительность дня 7 октября?
2) В пакете было 350 г сахара. Когда в него добавили ещё сахара, в нём стало 900 г. Сколько граммов сахара добавили в пакет?
3) На первой остановке в пустой автобус вошли несколько человек. На второй остановке вошли 10 человек, а на третьей – вышли 12 человек, после чего в автобусе осталось 17 человек. Сколько человек вошли в автобус на первой остановке?
№ 398. Мотоциклист едет из города в село, расстояние до которого 120 км. Сколько километров ему осталось проехать, если он уже проехал а км? Составьте выражение и найдите его значение при а = 40; 60; 80.
№ 399. Взрослый билет в музей стоит 150 р., а детский (для школьника) – 40 р. Если вместо 3 взрослых билетов приобрести билеты на дюжину школьников (дюжина – 12) и одного взрослого сопровождающего, то сколько нужно доплатить в кассу?
№ 400. Имелось 65 л фруктового сока. Из них 20 л дали детям во время завтрака, а остальной сок разлили в трёхлитровые банки. Сколько банок для этого потребовалось?
ОТВЕТ: 15 банок.
№ 401. Запишите все трёхзначные числа, которые можно записать только с помощью цифр 5, 3 и 0.
№ 402. Масса 11 ящиков яблок 4 ц 62 кг, а масса 18 ящиков груш 6 ц 12 кг. На сколько килограммов масса одного ящика яблок больше массы одного ящика груш?

ОТВЕТ: на 8 кг.
№ 403. Найдите значение выражения:
а) (37 296 : 37 – 17 780 : 35) : 250;
б) (504 • 370 – 158 092) : 47 + 1612.
Вы смотрели: Математика 5 Виленкин Упражнения 372-403 к учебнику математики с ответами. Решения задач из учебника УМК Виленкин и др. по теме «10. Уравнение».