Математика 5 Виленкин Учебник §2

2019 Математика 5 Виленкин Учебник §2 Сложение и вычитание натуральных чисел (Сложение натуральных чисел и его свойства. Вычитание. Числовые и буквенные выражения. Буквенная запись свойств сложения и вычитания. Уравнение).  Ознакомительная версия перед покупкой.

Математика 5 класс. УМК Виленкин и др. Учебник

§ 2. Сложение и вычитание натуральных чисел

6. Сложение натуральных чисел и его свойства

Ключевые слова: слагаемое, сумма, переместительное свойство сложения, сочетательное свойство сложения, свойство нуля, периметр многоугольника.

Если прибавить к натуральному числу единицу, то получится следующее за ним число. Например, 6 + 1 = 7; 99 + 1 = 100. Сложить числа 5 и 3 – значит прибавить к числу 5 три раза единицу. Получим: 5 + 3 = 5 + 1 + 1 + 1= 6 + 1 + 1= 7 + 1 = 8. Пишут короче: 5 + 3 = 8.

Числа, которые складывают, называют слагаемыми; число, получающееся при сложении этих чисел, называют их суммой. В записи 5 + 3 = 8 числа 5 и 3 – слагаемые, а число 8 – сумма. Сложение чисел можно изобразить на координатном луче (рис. 31).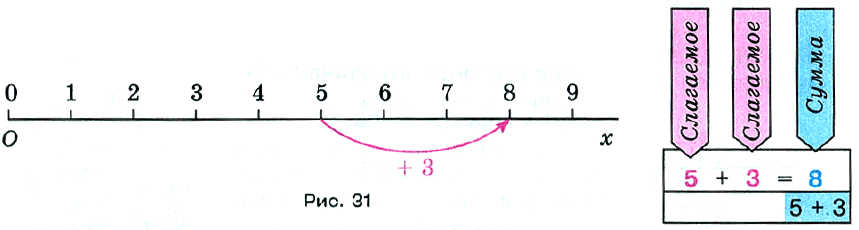

Мы знаем следующие свойства сложения:

1) Переместительное свойство сложения: сумма чисел не изменяется при перестановке слагаемых. Например: 5 + 4 = 9 и 4 + 5 = 9. Это свойство сложения называют переместительным (рис. 32).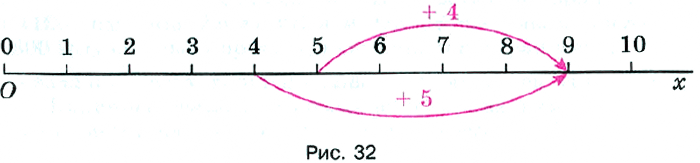

2) Сочетательное свойство сложения: чтобы прибавить к числу сумму двух чисел, можно сначала прибавить первое слагаемое, а потом к полученной сумме – второе слагаемое. Например, 3 + (8 + 6) = 3 + 14 = 17 и (3 + 8) + 6 = 11 + 6 = 17. Это свойство сложения называют сочетательным (рис. 33).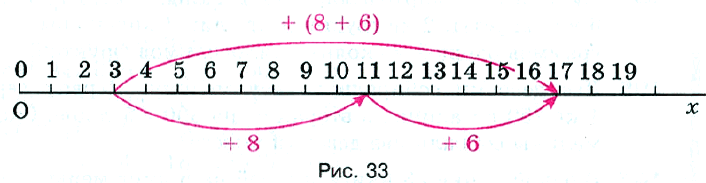

3) Свойство нуля: от прибавления нуля число не изменяется. Например, 9 + 0 = 9 (рис. 34). Так как 9 + 0 = 0 + 9, то и 0 + 9 = 9. Значит, если прибавить к нулю какое–нибудь число, то получится прибавленное число.

Вместо (5 + 9) + 7 пишут короче: 5 + 9 + 7. Когда в записи суммы нет скобок, то сложение выполняют по порядку слева направо.

Если точка С лежит на отрезке АВ, то длина всего отрезка АВ равна сумме длин его частей АС и СВ. Пишут: АВ = АС + СВ.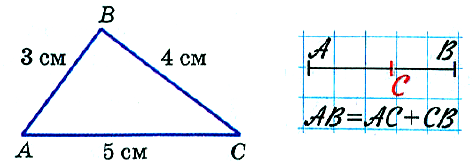

Сумму длин сторон многоугольника называют периметром этого многоугольника. Если в треугольнике АВС АВ = 3 см, ВС = 4 см и СА = 5 см, то периметр треугольника АВС равен 3 + 4 + 5, то есть 12 см.

ВОПРОСЫ к п.6

Какое число надо прибавить к натуральному числу, чтобы получилось следующее за ним число?
Какие числа называют слагаемыми?
Что называют суммой двух чисел?
Сформулируйте переместительное свойство сложения.
Сформулируйте сочетательное свойство сложения.
Изменяется ли число, если к нему прибавить нуль?
Чему равна сумма нуля и числа?
Что такое периметр треугольника?

УПРАЖНЕНИЯ (182–241)

7. Вычитание

Ключевые слова: уменьшаемое, вычитаемое, разность, свойства вычитания.

Задача. Пешеход за два часа прошёл 9 км. Сколько он прошёл за первый час, если его путь за второй час равен 4 км?

В этой задаче число 9 является суммой двух чисел, одно из которых равно 4, а другое неизвестно. Действие, с помощью которого по сумме и одному из слагаемых находят другое слагаемое, называют вычитанием. Так как 5 + 4 = 9, то искомое слагаемое равно 5. Значит, за первый час пешеход прошёл 5 км. Пишут: 9 – 4 = 5.

Число, из которого вычитают, называют уменьшаемым, а число, которое вычитают, – вычитаемым. Результат вычитания называют разностью. При вычитании 9 – 4 = 5 число 9 – уменьшаемое, 4 – вычитаемое, 5 – разность.

При действиях с натуральными числами уменьшаемое не может быть меньше вычитаемого.

Разность двух чисел показывает, на сколько первое число больше второго, иными словами, на сколько второе число меньше первого. На рисунке 35 вычитание 4 из 9 показано на координатном луче.

В следующих примерах результаты вычислений одинаковы:
12 – (3 + 2) = 12 – 5 = 7;
(12 – 3) – 2 = 9 – 2 = 7.

Свойства вычитания:

1. Для того чтобы вычесть сумму из числа, можно сначала вычесть из этого числа первое слагаемое, а потом из полученной разности – второе слагаемое. Это свойство называют свойством вычитания суммы из числа (рис. 36).
   
   

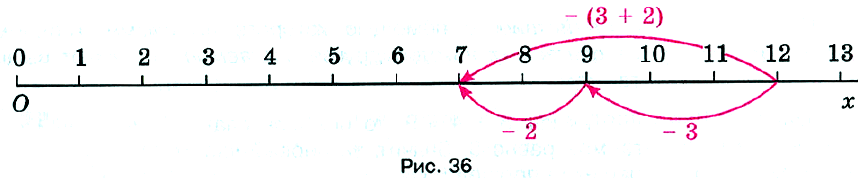
В следующих примерах результаты вычисления тоже одинаковы:
(6 + 3) – 2 = 9 – 2 = 7;
6 + (3 – 2) = 6 + 1 = 7;
(6 –2) + 3 = 4 + 3 = 7.

2. Чтобы из суммы вычесть число, можно вычесть его из одного слагаемого, а к полученной разности прибавить другое слагаемое. Конечно, вычитаемое число должно быть меньше слагаемого, из которого его вычитают, или равно ему. Это свойство называют свойством вычитания числа из суммы (рис. 37).
   
   

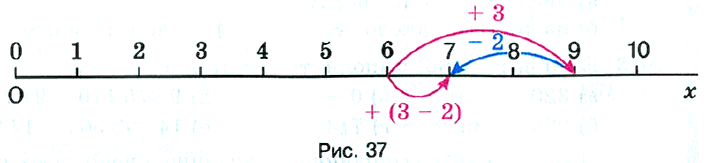
Так как 6 + 0 = 6, то по смыслу вычитания имеем: 6 – 0 = 6 (рис. 38) и 6 – 6 = 0 (рис. 39).

3. Если из числа вычесть нуль, оно не изменится.
4. Если из числа вычесть это число, получится нуль.

ВОПРОСЫ к п.7

Какое действие называют вычитанием?
Какое число называют уменьшаемым, а какое – вычитаемым? Как называют результат вычитания?
Как узнать, на сколько одно число больше другого?
Изобразите на координатном луче вычитание числа 3 из 8. Сформулируйте свойство вычитания суммы из числа. Сформулируйте свойство вычитания числа из суммы.
Поясните эти свойства вычитания на координатном луче.

УПРАЖНЕНИЯ (242–296)

8. Числовые и буквенные выражения

Ключевые слова: числовое выражение, значение выражения, буквенное выражение.

При решении задач иногда только записывают действия, а выполняют их потом. Полученные записи называют числовыми выражениями.

Задача 1. Поезд шёл двое суток. В первые сутки он прошёл 980 км, а во вторые – на 50 км больше. Сколько километров прошёл поезд за двое суток?

Решение. Во второй день поезд прошёл 980 + 50 километров. Значит, за два дня он прошёл 980 + (980 + 50) километров. Для решения задачи мы составили числовое выражение 980 + (980 + 50). Выполнив действия, получим число 2010 – значение этого выражения. Итак, за 2 дня поезд прошёл 2010 км.

Число, получаемое в результате выполнения всех указанных действий в числовом выражении, называют значением этого выражения.

Задача 2. Поезд шёл двое суток. В первые сутки он прошёл 980 км, а во вторые – на 65 км больше. Сколько километров прошёл поезд за двое суток?

Выражением для решения этой задачи будет 980 + (980 + 65). Его значение равно 2025. За два дня поезд прошёл 2025 км.

Задачи 1 и 2 отличаются лишь тем, что в задаче 2 число 50 заменено числом 65. Обозначим буквой m число, которое меняется от задачи к задаче. Получаем новую задачу.

Задача 3. Поезд шёл двое суток. В первые сутки он прошёл 980 км, а во вторые – на m км больше. Сколько километров прошёл поезд за двое суток?

Выражением для решения этой задачи будет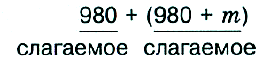

Если вместо буквы m подставить число 50, то получится числовое выражение для решения первой задачи. Если же вместо той же буквы подставить число 65, то получится числовое выражение для решения второй задачи.

Выражение, содержащее буквы, называют буквенным выражением. В этом выражении буквы могут обозначать различные числа. Числа, которыми заменяют букву, называют значениями этой буквы.

ВОПРОСЫ к п.8

Приведите пример числового выражения.
Как найти значение числового выражения?
Какое выражение называют буквенным?
Приведите пример буквенного выражения.

УПРАЖНЕНИЯ (297–336)

9. Буквенная запись свойств сложения и вычитания

Известные вам свойства сложения и вычитания можно записать с помощью букв.

1. Переместительное свойство сложения записывают так: а + b = b + а. В этом равенстве буквы а и b могут принимать любые натуральные значения и значение 0.
2. Сочетательное свойство сложения записывают с помощью букв так: a + (b + с) = (а + b) + с = a + b + с. Здесь а, b и с – любые натуральные числа или нуль.
3. Свойство нуля при сложении можно записать так: а + 0 = 0 + а = а. Здесь буква а может иметь любое значение.
4. Свойство вычитания суммы из числа записывают с помощью букв следующим образом: a – (b + с) = a – b – с. Здесь b + с < а или b + с = а.
5. Свойство вычитания числа из суммы записывают с помощью букв так:
   (а + b) – с = а + (b – с), если с < b или с = b.
   (а + b) – с = (а – с) + b, если с < а или с = а.
6. Свойства нуля при вычитании можно записать так: а – 0 = а; а – а = 0. Здесь а может принимать любые натуральные значения и значение 0.

Прочитайте записанные с помощью букв свойства сложения и вычитания.

УПРАЖНЕНИЯ (337–371)

10. Уравнение

Ключевые слова: уравнение, корень уравнения, решение уравнения, неизвестное слагаемое.

Задача. На левой чашке весов лежат арбуз и гиря в 2 кг, а на правой чашке – гиря в 5 кг Весы находятся в равновесии. Чему равна масса арбуза?

Решение. Обозначим неизвестную массу арбуза буквой х. Так как весы находятся в равновесии, должно выполняться равенство х + 2 = 5. Нам надо найти такое значение х, при котором выполняется это равенство. По смыслу вычитания, таким значением будет разность чисел 5 и 2, то есть 3. Значит, масса арбуза равна 3 кг. Пишут: х = 3. Если в равенство входит буква, то равенство может быть верным при одних значениях этой буквы и неверным при других её значениях. Например, равенство х + 2 = 5 верно при х = 3 и неверно при х = 4.

Уравнением называют равенство, содержащее букву, значение которой надо найти.

Значение буквы, при котором из уравнения получается верное числовое равенство, называют корнем уравнения. Например, корнем уравнения х + 2 = 5 является число 3.

Решить уравнение – значит найти все его корни (или убедиться, что это уравнение не имеет ни одного корня).

Пример 1. Решим уравнение х + 12 = 78.

Решение. По смыслу вычитания, неизвестное слагаемое равно разности суммы и другого слагаемого. Поэтому х = 78 – 12, то есть х = 66. Число 66 является корнем уравнения х + 12 = 78, потому что 66 + 12 = 78. Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое (рис. 44, а).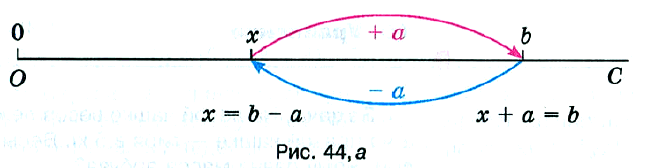

Пример 2. Решим уравнение у – 8 = 11.

Решение. По смыслу вычитания, у является суммой чисел 11 и 8. Значит, у = 11 + 8, то есть у = 19. Число 19 является корнем уравнения у – 8 = 11, так как верно равенство 19 – 8 = 11. Чтобы найти неизвестное уменьшаемое, надо сложить вычитаемое и разность (рис. 44, б).

Пример 3. Решим уравнение 15 – z – 9.

Решение. По смыслу вычитания, число 15 является суммой г и 9, то есть z + 9 = 15. Из этого уравнения находим неизвестное слагаемое: z = 15 – 9, то есть z = 6. Число 6 является корнем уравнения 15 – z = 9, так как верно равенство 15 – 6 = 9. Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность (рис. 44, в).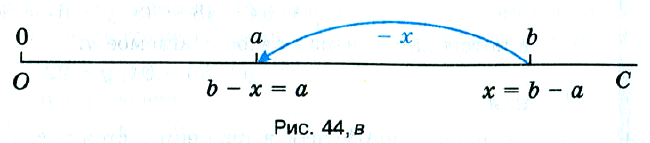

ВОПРОСЫ к п.10

Какое равенство называют уравнением?
Какое число называют корнем уравнения?
Что значит решить уравнение?
Как проверить, верно ли решено уравнение?
Как найти неизвестное слагаемое; вычитаемое; уменьшаемое?

УПРАЖНЕНИЯ (372–403)

Задания для самопроверки

Темы проектных работ

1. Как в старину считали на Руси?
2. Счёт у народов мира.

Вы смотрели: Математика 5 Виленкин Учебник §1 Натуральные числа и шкалы (Обозначение натуральных чисел. Отрезок. Длина отрезка. Треугольник. Плоскость. Прямая. Луч. Шкалы и координаты. Меньше или больше).