Учебное пособие по математике для 5 класса (2019 г.) Глава 1. Натуральные числа (§1 Ряд натуральных чисел. §2 Цифры. Десятичная запись натуральных чисел. §3 Отрезок. Длина отрезка. §4 Плоскость. Прямая. Луч. §5 Шкала. Координатный луч. §6 Сравнение натуральных чисел). Математика Мерзляк Учебник Гл 1. Ознакомительная версия перед покупкой. Цитаты из пособия использованы в учебных целях.
Математика 5 класс. УМК Мерзляк. Учебник
Глава 1. Натуральные числа
Познакомитесь со свойствами прямой, луча и отрезка.
§ 1. Ряд натуральных чисел
Сколько дней осталось до конца каникул? Сколько друзей вы пригласите на свой день рождения? Сколько предметов вы изучаете в этом учебном году? Чтобы ответить на эти вопросы, необходимо уметь считать.
Числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 и т. д., используемые при счёте предметов, называют натуральными.
Например, числа 1, 3, 24, 60, 365, 1 000 000 — натуральные числа. Заметьте, что не все числа, которыми вы пользуетесь, — натуральные. Так, числа 0, 1/2, 2/3 натуральными не являются.
Все натуральные числа, записанные в порядке возрастания, образуют ряд натуральных чисел (или натуральный ряд). Первым числом натурального ряда является число 1, вторым — число 2, третьим — число 3 и т. д.
В натуральном ряду за каждым числом следует ещё одно число, большее предыдущего на единицу. Поэтому в натуральном ряду нет последнего числа. Число 1 не имеет предыдущего. Следовательно, среди натуральных чисел есть наименьшее число — это число 1, но нет наибольшего.
Выписать весь натуральный ряд невозможно. Обычно поступают так: выписывают подряд несколько первых чисел натурального ряда, а затем ставят многоточие: 1, 2, 3, 4, 5, 6. 7, 8, 9, 10, 11, 12, … .
§ 2. Цифры. Десятичная запись натуральных чисел
Как здание строят из кирпичей, а слова складывают из букв, так натуральные числа записывают с помощью специальных знаков, которые называют цифрами. Этих цифр десять: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Натуральные числа, записанные одной цифрой, называют однозначными, двумя цифрами двузначными, тремя цифрами — трёхзначными и т. д. Все числа, кроме однозначных, называют многозначными. Многозначное число может начинаться с любой цифры, кроме цифры 0.
Легко прочитать трёхзначное число 917, однако число 17025543607 прочитать намного сложнее. Чтобы прочитать многозначное число, цифры его записи разбивают справа налево на группы по три цифры: 17 025 543 607 (при этом крайняя слева группа может состоять из трёх цифр, из двух, как в данном примере, или из одной цифры). Эти группы называют классами. Первый справа класс называют классом единиц, второй справа — классом тысяч, третий — классом миллионов, четвёртый — классом миллиардов и т. д.
При чтении многозначного числа число, записанное в каждом классе, читают как трёхзначное, двузначное или однозначное, добавляя при этом название класса (как правило, название класса единиц не произносят). Число 17 025 543 607 читают: «17 миллиардов 25 миллионов 543 тысячи 607».
Если все цифры какого–то класса числа являются нулями, то, читая число, название этого класса не произносят. Например, число 2 000 724 читают: «два миллиона семьсот двадцать четыре».
Каждый класс разбивается справа налево на три разряда: единицы, десятки, сотни.
Так, в приведённом примере в классе единиц 7 единиц, 0 десятков, 6 сотен, а в классе миллионов — 5 единиц, 2 десятка, 0 сотен. Названия всех разрядов числа 17 025 543 607 приведены в следующей таблице.
Запись натуральных чисел, которой мы пользуемся, называют десятичной. Такое название связано с тем, что десять единиц каждого разряда составляют одну единицу следующего, старшего разряда. Например, десять единиц составляют один десяток, десять десятков — одну сотню и т. д.
Число 2 958 можно представить в виде суммы:
2 958 = 2 000 + 900 + 50 + 8
или
2 958 = 2 • 1 000 + 9 -• 100 + 5 • 10 + 8 • 1.
Последнее равенство называют записью числа 2 958 в виде суммы разрядных слагаемых.
Когда сделаны уроки
Как считали в старину
В местах обитания первобытного человека археологи находят предметы с выбитыми точками, нацарапанными чёрточками, глубокими зарубками. Эти находки позволяют предположить, что уже в каменном веке люди умели не только считать, но и фиксировать результаты своих подсчётов.
С развитием общества совершенствовались и способы счёта. Ведь такие примитивные приёмы, как зарубки на палке, узлы на верёвке или камешки, сложенные в кучки, не могли удовлетворить потребности торговли и производства.
Приблизительно за 3 000 лет до нашей эры было сделано важнейшее открытие: люди изобрели специальные знаки для обозначения некоторого количества предметов. Например, египтяне десяток обозначали знаком ∩, сотню — ⊂. Так, число 123 записывалось следующим образом: ⊂∩∩III.
В Древнем Риме записывали числа с помощью таких цифр: I — один, V — пять, X — десять, L пятьдесят, С — сто, D — пятьсот, М — тысяча.
Римская система счисления основывается на следующем принципе: если при чтении слева направо меньшая цифра стоит после большей, то она прибавляется к большей: VI = 6, XXXII = 32; если меньшая цифра стоит перед большей, то она вычитается из большей: IV = 4, VL = 45.
В римской системе счисления, например, число 14 записывают так: XIV. Здесь цифра I стоит между двумя большими цифрами X и V. В таких случаях цифру I вычитают из цифры, стоящей от неё справа (в нашем примере это цифра V).
Год, в котором завершилась победой нашего народа Великая Отечественная война, с помощью римских цифр можно записать так: MCMXLV.
Эта система сохранилась и до наших дней. Часто можно встретить записи, в которых используются римские цифры, например: XXI век, глава VI. Также их можно увидеть на циферблатах часов, на памятниках архитектуры.
Вы, наверное, уже заметили, что даже прочитать число, записанное римскими цифрами, непросто. Тем более сложно выполнять в такой записи арифметические действия. Кроме того, если требуется записывать достаточно большие числа (миллион, миллиард и т. д.), то нужно придумывать новые цифры. В противном случае запись числа будет очень длинной. Например, если для записи числа 1 000 000 использовать только римскую цифру М, то запись будет состоять из тысячи таких знаков. Все эти недостатки существенно сужают возможность применения римской системы счисления.
В Древней Руси не стали выдумывать специальные значки для обозначения цифр. Их получали с помощью букв алфавита. Над буквой ставили волнистую линию — титло ( ҃). Например, число 241 записывали так: с҃ м҃ а҃.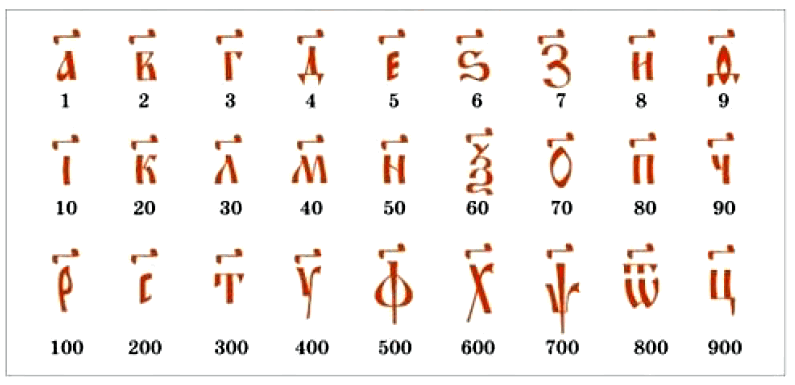
Величайшим достижением человечества является изобретение десятичной позиционном системы счисления. С помощью этой системы записывают сколь угодно большие числа, используя всего лишь десять различных цифр. Это возможно потому, что одна и та же цифра имеет различные значения в зависимости от её позиции в числе.
Цифры 0, 1,2, 3, 4, 5, 6, 7, 8, 9 называют арабскими. Однако арабы лишь распространили десятичную позиционную систему, изобретённую индусами.
Некоторые племена и народы использовали другие позиционные системы счисления. Например, индейцы племени майя использовали двадцатеричную систему, а древний народ шумеры — шестидесятеричную.
Следы двадцатеричной системы можно обнаружить в некоторых европейских языках. Так, французы вместо «восемьдесят» говорят «четырежды двадцать» (quatrc–vingts). Разбиение одного часа на 60 минут, а одной минуты на 60 секунд пример явного наследия шестидесятеричной системы.
Счёт с помощью десяти пальцев рук привёл к возникновению десятичной системы. Общее количество пальцев на руках и ногах явилось основой для создания двадцатеричной системы. «Пальцевое» происхождение имеет и двенадцатеричная система: попробуйте большим пальцем руки сосчитать фаланги на других пальцах этой же руки, в результате получится число 12 (рис. 2). Так возник счёт дюжинами. И в наши дни в Европе дюжинами продают носовые платки, пуговицы, куриные яйца.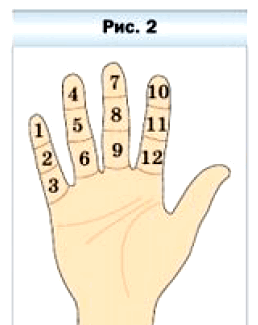
Количество предметов в столовых приборах и сервизах (вилки, ножи, ложки, тарелки, чашки, бокалы и т. и.), как правило, равно 6 (полудюжина), 12, 24 и т. д.
Существуют и другие позиционные системы счисления. Так, в основе строения и работы компьютера лежит двоичная система счисления, использующая лишь две цифры — 0 и 1. Более подробно о двоичной системе счисления вы узнаете на уроках информатики.
Как называют «числа–великаны»
Число миллион — большое или маленькое? Например, чтобы провести на уроках один миллион минут, вам пришлось бы учиться в школе около 20 лет. Этот пример показывает, что миллион — большое число.
Однако для удовлетворения потребностей таких наук, как экономика, астрономия, физика, химия, нужны числа гораздо больше миллиона.
Тысячу миллионов называют биллионом, или миллиардом, тысячу биллионов — триллионом. Если к триллиону приписать справа три нуля, то получим квадриллион. Далее, приписывая каждый раз по три нуля, получим последовательность чисел с такими названиями: квинтиллион, секстиллион, септиллион, октиллион, нониллион. Есть названия и у чисел, больших нониллиона.
Чтобы вы могли представить, насколько эти числа огромны, приведём ещё один пример. Возраст нашей Вселенной, по оценкам учёных, не превосходит квинтиллиона минут.
§ 3. Отрезок. Длина отрезка
Если вы хорошо заточенным карандашом прикоснётесь к тетрадному листу, то останется след, который даёт представление о точке (рис. 3). Точки принято обозначать прописными латинскими буквами: А, В, С, … .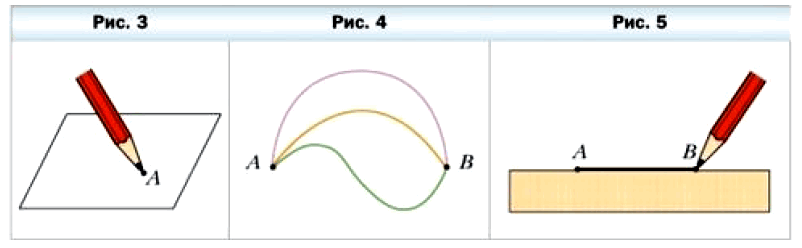
Отметим на листе бумаги две точки А и В. Эти точки можно соединить различными линиями (рис. 4). А как соединить точки А и В самой короткой линией? Это можно сделать с помощью линейки (рис. 5). Полученную линию называют отрезком, а точки А и В — концами отрезка.
Точка и отрезок — примеры геометрических фигур.
Существует единственный отрезок, концами которого являются точки А и В. Поэтому отрезок обозначают, записывая точки, которые являются его концами. Например, отрезок на рисунке 5 обозначают одним из двух способов: АВ или ВА. Читают: «отрезок АВ» или «отрезок ВА».
На рисунке 6 изображены три отрезка. Длина отрезка АВ равна 1 см. Он помещается в отрезке MN ровно три раза, а в отрезке ЕЕ ровно четыре раза. Будем говорить, что длина отрезка MN равна 3 см, а длина отрезка ЕF = 4 см.
Также принято говорить: «отрезок MN равен 3 см», «отрезок ЕF равен 4 см». Пишут: MN = 3 см, ЕЕ = 4 см.
Длины отрезков MN и ЕЕ мы измерили единичным отрезком, длина которого равна 1 см. Для измерения отрезков можно выбрать и другие единицы длины, например: 1 мм, 1 дм, 1 км. На рисунке 7 длина отрезка РК равна 17 мм. Он измерен единичным отрезком, длина которого равна 1 мм, с помощью линейки с делениями. Также с помощью линейки можно построить (начертить) отрезок заданной длины (см. рис. 7).
Вообще, измерить отрезок означает подсчитать, сколько единичных отрезкой в нём помещается.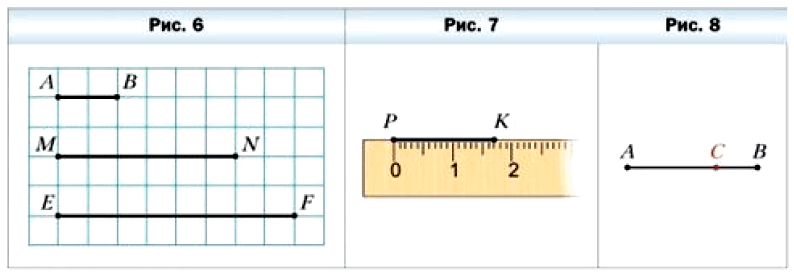
Длина отрезка обладает следующим свойством: Если на отрезке АВ отметить точку С, то длина отрезка АВ равна сумме длин отрезков АС и СВ (рис. 8). Пишут: АВ = АС + СВ.
На рисунке 9 изображены два отрезка АВ и СD. Эти отрезки при наложении совпадут.
Два отрезка называют равными, если они совпадают при наложении.
Следовательно, отрезки АВ и СD равны. Пишут: АВ = СD.
Равные отрезки имеют равные длины.
Из двух неравных отрезков большим будем считать тот, у которого длина больше. Например, на рисунке 6 отрезок EF больше отрезка MN.
Длину отрезка АВ называют расстоянием между точками A и В.
Если несколько отрезков расположить так, как показано на рисунке 10, то получится геометрическая фигура, которую называют ломаной. Заметим, что все отрезки на рисунке 11 ломаную не образуют. Считают, что отрезки образуют ломаную, если конец первого отрезка совпадает с концом второго, а другой конец второго отрезка — с концом третьего и т. д.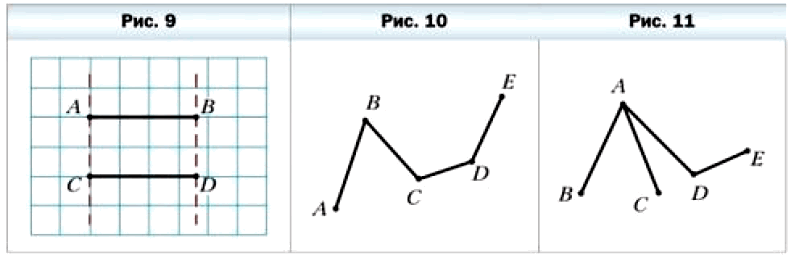
Точки A, В, С, D, Е — вершины ломаной ABCDE, точки А и Е — концы ломаной, а отрезки АВ, ВС, СП, ПЕ — её звенья (см. рис. 10). Длиной ломаной называют сумму длин всех её звеньев.
На рисунке 12 изображены две ломаные, концы которых совпадают. Такие ломаные называют замкнутыми.
Пример 1. Отрезок ВС на 3 см меньше отрезка АВ, длина которого равна 8 см (рис. 13). Найдите длину отрезка АС.
Решение. Имеем: ВС = 8 – 3 = 5 (см). Воспользовавшись свойством длины отрезка, можно записать АС = АВ + ВС. Отсюда АС = 8 + 5 = 13 (см).
Ответ: 13 см. ◄
Пример 2. Известно, что МК = 24 см, NP = 32 см, МР = 50 см (рис. 14). Найдите длину отрезка NК.
Решение. Имеем: MN = МР – NP. Отсюда MN = 50 – 32 = 18 (см). Имеем: NK = МК – MN. Отсюда NK = 24 – 18 = 6 (см).
Ответ: 6 см. ◄
Вопросы на стр.19 (с ответами)
Когда сделаны уроки
От локтей и ладоней к метрической системе
Для измерения длины отрезка каждый ученик вашего класса может на своё усмотрение выбрать в качестве единичного отрезок любой длины. Однако в этом случае будет довольно трудно совместно пользоваться результатами измерений. Гораздо удобнее согласовать свой выбор, т. е. указать отрезок, которым при измерениях будут пользоваться все. Приблизительно так и возникли единицы измерения длины.
Испокон веков люди пользовались такой естественной мерой длины, как шаг. Многие народы применяли меру длины дальность полёта стрелы. Большие расстояния измеряли дневными переходами. Также использовали «измерительные приборы», которые были под рукой: дюйм, ладонь, пядь (рис. 33, а), локоть, фут (рис. 33, 6), косая сажень (рис. 33, в) и т. д.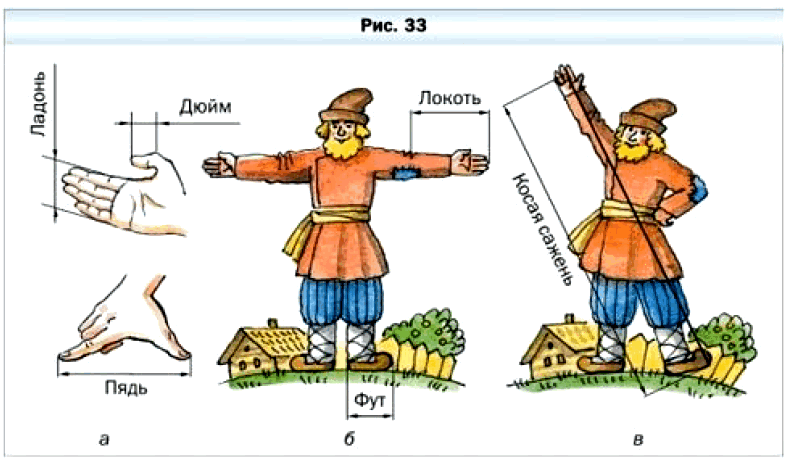
Понятно, что такие «эталоны» длины удобны, но очень неточны. Кроме того, их многообразие и несогласованность были преградой в общении, развитии торговли и производства. Так, в XVIII в. почти каждый немецкий город, большинство провинций Италии вводили свои меры длины, которые нередко имели одинаковые названия, но не были равны. Во Франции дело дошло до того, что каждый феодал устанавливал в своих владениях собственные меры.
В 1790 г. в Национальное собрание Франции было внесено предложение о создании новой системы мер, и в 1791 г. была введена единица длины — метр. Слово «метр» происходит от греческого слова «метрон», что означает «мера». В 1799 г. был изготовлен эталон метра (рис. 34) в виде платинового стержня. Однако понадобилось ещё почти 100 лет, чтобы метрическая система мер заняла в Европе прочное положение.
Названия других единиц длины, связанных с метром, образованы с помощью приставок деци–, санти–, милли–, что означает уменьшение метра соответственно в 10, 100, 1 000 раз. Например, дециметр — десятая часть метра, миллиметр тысячная часть метра. Приставка кило– означает увеличение в 1 000 раз, поэтому километр равен 1 000 метров.
В России метрическую систему мер начали вводить с конца XIX в. Большая заслуга в её распространении принадлежит великому русскому химику Дмитрию Ивановичу Менделееву.
Метрическая система мер введена в большинстве стран мира, однако не во всех странах. Например, в Англии до сих пор пользуются такими средневековыми мерами длины, как миля, ярд, фут, дюйм. На стене обсерватории в Гринвиче изображены эталоны длины (рис. 35).
§ 4. Плоскость. Прямая. Луч
Размеры тетради не позволяют строить отрезки большой длины. А вообразите себе, что тетрадный лист вырос до размеров стола, теннисного корта, даже футбольного поля. Такой лист является примером или, как ещё принято говорить, моделью части плоскости.
Плоскость бесконечна, поэтому её нельзя изобразить. Эту геометрическую фигуру можно вообразить.
Теперь понятно, что на плоскости можно начертить отрезок очень большой длины. Более того, любой отрезок с помощью линейки можно продлить в обе стороны. Мысленно это можно сделать неограниченно, и тогда мы получим геометрическую фигуру, которую называют прямой.
Прямая не имеет концов. Она бесконечна. Поэтому на рисунке мы изображаем только часть прямой — отрезок.
Отметим на листе бумаги две точки А и В. Проведём через них прямую (рис. 36, а). Если попытаемся провести через эти точки ещё одну прямую, то нам это не удастся.
Через две точки проходит только одна прямая.
Это свойство позволяет обозначать прямую, называя две любые её точки. Так, прямую, изображённую на рисунке 36, а, обозначают одним из двух способов: АВ или ВА. Читают: «прямая АВ» или «прямая ВА».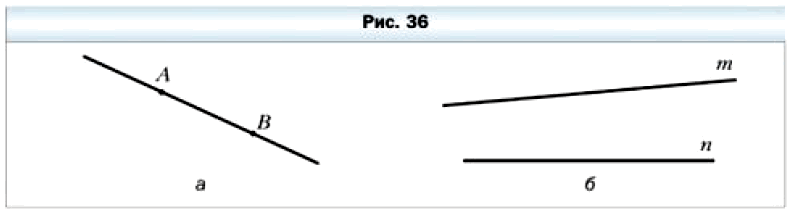
Прямые также обозначают одной строчной латинской буквой. На рисунке 36, 6 изображены прямые m и n.
Проведём прямую А В и отметим на ней точку О (рис. 37, а). Эта точка делит прямую на две части. Каждую из этих частей вместе с точкой О называют лучом с началом в точке О. Конца у луча нет.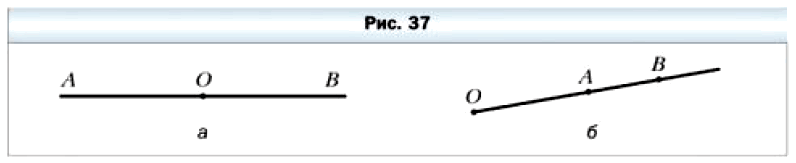
Так же, как и прямую, луч обозначают двумя прописными буквами. Сначала записывают букву, обозначающую начало луча, а йотом букву, обозначающую какую–либо другую точку этого луча. Например, луч с началом в точке О (рис. 37, 6) можно обозначить ОА или ОВ.
Луч — это ещё один пример геометрической фигуры.
Вопросы на стр.29 (с ответами)
Упражнения 85-111 (с ответами)
Когда сделаны уроки
О льняной нити и линиях
Отрезок, прямая, луч — это примеры линий. След, оставленный коньками фигуриста на льду (рис. 43, а), нитка, случайно оказавшаяся на вашей одежде, дают представление о линии. Автомобильную дорогу на карте изображают в виде линии (рис. 43, б).
Древнегреческий математик Евклид в своей знаменитой книге «Начала» образно определил линию как «длину без ширины». Слово «линия» происходит от латинского слова linum — «лён», «льняная нить».
С помощью остро заточенного карандаша вы можете нарисовать очень замысловатую линию, например сконструировать личную подпись. Так, на рисунке 44 представлено изображение (факсимиле) подписи выдающегося русского математика Н. И. Лобачевского.
На рисунке 45 изображены: а — окружность, 6 — эллипс, в — парабола, г — спираль (от греч. «спира» — «виток»), д — лемниската (от греч. «лемнискус» — «бант»), е — кардиоида (от греч. «кардиа» — «сердце»), ж — астроида (от греч. «астрон» — «звезда»), э — циклоида (от греч. «киклоидес» — «кругообразный»), и — клофоида (от греч. «клофо» — «прясть»).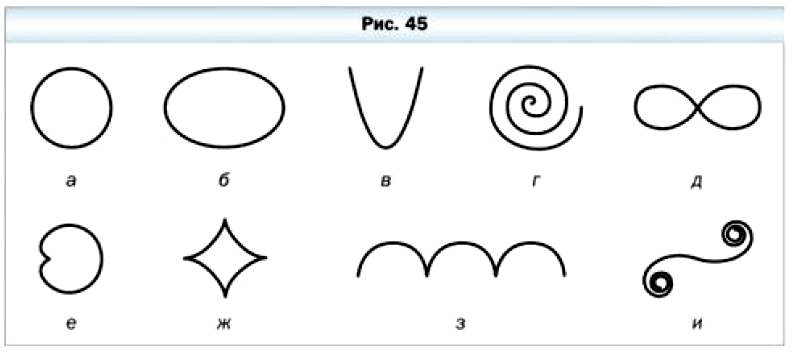
Семейство линий очень многообразно. Со свойствами некоторых из них вы подробнее познакомитесь в старших классах.
§ 5. Шкала. Координатный луч
С помощью ровной деревянной рейки две точки А и В можно соединить отрезком (рис. 46). Однако этим примитивным инструментом измерить длину отрезка AB не удастся. Его можно усовершенствовать.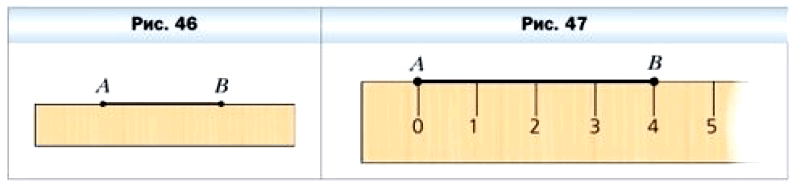
На рейке через каждый сантиметр нанесём штрихи. Под первым штрихом напишем число 0, под вторым — 1, под третьим — 2 и т. д. (рис. 47). В таких случаях говорят, что на рейку нанесена шкала с ценой деления 1 см. Эта рейка со шкалой похожа на линейку. Но чаще всего на линейку наносят шкалу с ценой деления 1 мм (рис. 48).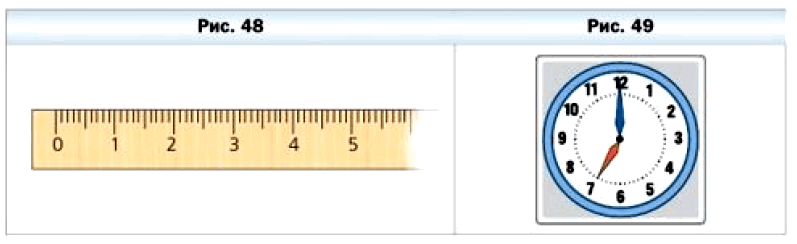
Из повседневной жизни вам хорошо известны и другие измерительные приборы, имеющие шкалы различной формы. Циферблат часов — это шкала с ценой деления 1 мин (рис. 49). На рисунке 50 изображён спидометр автомобиля со шкалой, цена деления которой 10 км/ч. Комнатный термометр (рис. 51), весы (рис. 52) — также приборы со шкалами, деления которых соответственно равны 1 С и 50 г.
Конструктор создаёт измерительные приборы, шкалы которых конечны, т. е. среди отмеченных на шкале чисел всегда есть наибольшее. А вот математик с помощью воображения может построить и бесконечную шкалу.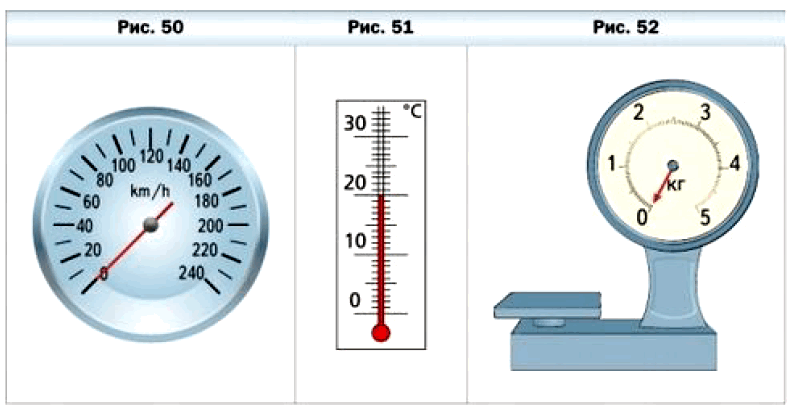
Начертим луч ОХ. Отметим на этом луче какую–нибудь точку Е. Напишем под точкой О число 0, а под точкой Е — число 1 (рис. 53).
Будем говорить, что точка О изображает число 0, а точка Е — число 1. Также принято говорить, что точке О соответствует число 0, а точке Е — число 1.
Отложим вправо от точки Е отрезок, равный отрезку ОЕ. Получим точку М, которая изображает число 2 (см. рис. 53). Таким же образом отметим точку N, изображающую число 3. Так, шаг за шагом, получаем точки, которым соответствуют числа 4, 5, 6, … . Мысленно этот процесс можно продолжать как угодно долго.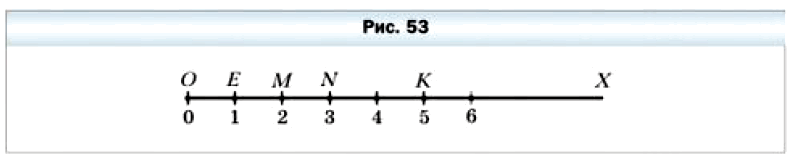
Полученную бесконечную шкалу называют координатным лучом, точку О — началом отсчёта, а отрезок ОЕ — единичным отрезком координатного луча.
На рисунке 53 точка К изображает число 5. Говорят, что число 5 является координатой точки К, и записывают К (5). Аналогично можно записать О (0), Е (1), M (2), N (3).
Часто вместо слов «отметим точку с координатой, равной…» говорят «отметим число…».
Вопросы на стр.36 (с ответами)
Упражнения 112-141 (с ответами)
§ 6. Сравнение натуральных чисел
Сравнить два различных натуральных числа — это значит определить, какое из них больше, а какое — меньше.
Из двух натуральных чисел меньшим является то, которое в натуральном ряду стоит раньше, а бо́льшим — то, которое в натуральном ряду стоит позже. Поэтому, например, число 5 меньше числа 7, а число 171 больше числа 19. Результаты сравнения записывают с помощью знаков < (меньше) и > (больше): 5 < 7 и 171 > 19. Такие записи называют неравенствами.
Число 0 меньше любого натурального числа. Например, 0 < 12.
Сравнивать можно одновременно и три числа. Например, число 17 больше 15, но меньше 20. Это записывают так: 15 < 17 < 20. Такую запись называют двойным неравенством. Часто слово «двойное» опускают, называя двойное неравенство неравенством.
Натуральные числа можно сравнивать, не обращаясь к натуральному ряду. Сравнивать многозначные числа, имеющие разное количество цифр, легко.
Из двух натуральных чисел, имеющих разное количество цифр, большим является то, у которого количество цифр больше.
Например, число 597 013 617 — девятизначное, а число 99 982 475 — восьмизначное, поэтому первое число больше второго. Если два многозначных числа имеют одинаковое количество цифр, то следует руководствоваться таким правилом.
Из двух натуральных чисел с одинаковым количеством цифр большим является то, у которого больше первая (при чтении слева направо) из неодинаковых цифр.
Например, 7 256 > 7 249, а 582 647 < 582 879.
Отметим, что на координатном луче точка с меньшей координатой расположена левее точки с большей координатой. Например, точка А (7) лежит левее точки В (9), так как 7 < 9 (рис. 63).
На координатном луче ил двух натуральных чисел меньшее число расположено левее большего.
Пример 1. В записи чисел вместо некоторых цифр поставили звёздочки. Сравните эти числа: 1) 69* и * *43; 2) 72 *** и 70 ***.
Решение. 1) Поскольку первое число трёхзначное, а второе – четырёхзначное, то 69* < * *43.
2) Цифр в этих числах поровну. Первая цифра каждого из них равна 7. Вторые цифры этих чисел равны соответственно 2 и 0. Поскольку 2 > 0, то 72 *** > 70 ***. ◄
Пример 2. Сравните 8 км 24 м и 8 146 м.
Решение. Поскольку 8 км 24 м = 8 024 м, то 8 км 24 м < 8 146 м. ◄
Вопросы на стр.42 (с ответами)
Упражнения 142-166 (с ответами)
Вы смотрели: Учебное пособие по математике для 5 класса (2019 г.) Глава 1. Натуральные числа (§1 Ряд натуральных чисел. §2 Цифры. Десятичная запись натуральных чисел. §3 Отрезок. Длина отрезка. §4 Плоскость. Прямая. Луч. §5 Шкала. Координатный луч. §6 Сравнение натуральных чисел). Математика Мерзляк Учебник Гл 1. Ознакомительная версия перед покупкой.